
Показана возможность нового принципа обработки многомерных динамических рядов на базе инструментального (компьютерного) моделирования. Видимо, массовое применение этого подхода в транспортно-градостроительных исследованиях поможет выявить, либо уточнить спектр ранее известных или вовсе неизвестных динамических закономерностей развития городов и агломераций.
В области градостроительной, прогнозной,
плановой и проектной деятельности обычно применяются
методы прямого счета и простых балансовых соотношений.
Динамические ряды редко используются в практической
деятельности. Кроме того, проектные расчеты и разнообразные
прикидки на перспективу совпадают с реальным развитием
на сроки более 5-7 лет только в виде исключения.
Целью данной работы является предложение использовать
мощный аппарат обработки долговременных динамических
многомерных рядов в виде оригинального эвристического
подхода. Дело в том, что обычные процедуры обработки
любых данных, основанные на теории вероятностей, налагают
жесткие требования, которые практически трудно выполнимы:
независимость и случайность анализируемых событий;
распределение значений этих событий по нормальному закону
распределения вероятностей.
При строгом следовании этим требованиям обработка динамических
рядов практически становится невозможной. Значит, корректное
использование математической статистики распро-страняется
только на статику. Однако запросы реальной жизни заставили
создать разнообразные обходные пути обработки рядов,
в которых единственным аргументом функции является историческое
время: гармоники Фурье, метод трендов, исключение автокорреляции,
обработка отклонения от трендов, спектрально-временной
анализ, вейвлет анализ, переменная корреляция трендов
и отклонений от них, метод спектрально-временных диаграмм,
эвристические подходы школы Index number и, так называемого,
технического анализа. Кроме того, с конца 70-х гг. развивается
моделирование динамических процессов в рамках таких
направлений, как эволюционная экономика и синергетика.
Имеются представления о цикличности многих природных
процессов, а также возможности их трансляции на социально-экономические
и даже политические процессы. Однако строгая периодичность
их не подтверждается эмпирически: обычно периоды размыты,
а главное, в каждом отдельном случае трудно определить
начало фаз цикла. Кроме того, параметры цикличности
меняются; эти изменения трудно описать аналитически
и, следовательно, предсказывать. В частности, неразрешимой
до недавнего времени задачей был прогноз солнечной активности
(чисел Вольфа и др.). В последнее десятилетие появились
модели зависимости параметров этой природной цикличности:
найдены соотношения между амплитудой цикла и его периодом.
Наоборот, в последние годы более детальный анализ так
называемых больших циклов экономической конъюнктуры
Кондратьева показал их недостаточную адекватность реальным
процессам. Одним словом, в вопросах прогнозирования
социально-экономических процессов историческое время,
в большинстве случаев, вообще невозможно принять в качестве
аргумента прогнозных функций. Следовательно, необходимо
оперировать реально действующими в динамике факторами.
Самая большая трудность заключается в том, что этих
главных факторов, как правило, много – 6-7.
В градостроительной области для анализа сложных процессов
главным образом нужны методы учета действия в динамике
факторов различной природы: экономических, технико-технологических,
планировочных, социально-психологических, экономических
и др. Синхронное и асинхронное развитие процессов под
влиянием этих разнообразных факторов и является главным
объектом возможного статистического анализа. Историческое
время, как таковое, не является действующим фактором,
оно образно является только свидетелем этих процессов.
Поэтому, ясно, что для адекватного анализа нужны принципиально
другие методы статистической обработки, учитывающей
динамическую многомерную сущность сложных динамических
процессов.
Следует заметить, что экономисты с математической подготовкой
у нас и за рубежом подошли к этой задаче еще в конце
XIX в. Обычно они пользовались стандартными методами
корреляционного анализа для двух разных динамических
рядов. Получая коэффициент корреляции, например 0,5
или 0,7, они считали задачу решенной. Сейчас совершенно
отчетливо ясно, что эти значения коэффициентов связи
или сопряженности были непригодны для практических расчетов.
Опыт подобных расчетов показал, что отклонения от фактов
(выбросы) по отдельным точкам даже при высоких коэффициентах
связи могут составлять более 100%.
В городах такой анализ необходимо доводить до конкретных
районов и кварталов, особенно в городах-миллионерах.
Какие-то общие тенденции, тренды и т.п. здесь не годятся,
нужны данные расчетов по синхронности и асинхронности
развития по отдельным достаточно мелким районам, подрайонам.
В транспортно-градостроительной практике впервые динамический
подход был предложен Фратаром в 1954 г.
Сейчас мы осветим существенно отличающийся метод прогнозирования
транспорта, путей сообщения, вообще любых других процессов
градостроительного характера, учитывающий трудно предвидимые
ввиду обратных нелинейных связей взаимозависимости между
факторами, влияющими на развитие градостроительных систем.
Движение к намеченной цели началось с выдвижения другого
критерия связности динамических рядов. Вместо коэффициентов
корреляции и детерминации было принято отклонение факта
от теории по каждой точке-наблюдению, т.е.
![]() ≤0,15
и
≤0,15
и ![]() ≤0,05
≤0,05
где уфi и утi – фактическое и теоретическое значение ряда;
n – количество наблюдений;
i – порядковый номер наблюдения.
Кроме того, статистические испытания
производятся до тех пор, пока распределение отклонений
не станет близким к нормальному. Помимо этого для создания
адекватного прогнозного фона необходимо брать достаточно
большую ретроспективу по всему множеству анализируемых
факторов: отношение данных за прошедший период к прогнозируемому
должен быть как минимум 5:1.
В этом подходе принципиально игнорируется феномен автокорреляции,
т.к. считается, что выполнение описанного выше критерия
гарантирует адекватность модельного представления дина-мического
процесса. Весь процесс моделирования может быть представлен
в виде следующих шагов:
a) на качественном уровне подбирается ансамбль действующих
на процесс развития факторов;
b) строится корреляционная матрица между ними;
c) выбираются по этой матрице только те коэффициенты
связи, которые численно более 0,9 (как правило, линейные
регрессии в сложных условиях градостроительных процессов
не удовлетворяют указанному критерию);
d) производится последующий перебор факторов, соответствующий
пункту (с);
e) при двух выбранных факторах, действующих на зависимую
переменную, вычисляется квадратичная поверхность, затем
рассчитываются отклонения от этой поверхности;
f) если не найдена хорошая связь, то каждая из осей
нагружается дополнительными переменными и выполняется
построение новой поверхности;
g) дополнительные возможности адекватного моделирования
появляются в том случае, если в отклонениях появляется
строго периодические компоненты; тогда имеется возможность
разбить весь ряд на несколько временных отрезков и повторить
процедуру, применив стандартный гармонический анализ
отклонений.
В качестве проверки предлагаемого подхода к моделированию
возьмем мало известные данные по протяженности улиц,
дорог, проездов, набережных в городских поселениях.
Эти данные в сводном виде по стране практически не публиковались
Госкомстатом. Тем не менее, в отдельных публикациях
разных авторов частично эти данные приведены. Все они
были систематизированы и приведены к сопоставимому виду.
Ниже представлены фактические данные по УДС СССР:
Чтобы восстановить недостающие данные по всем промежуточным
годам, использовалась гипотеза о возможной связи этих
данных с численностью общего и, в т.ч. городского населения.
Была применена двухфакторная динамическая модель (рис
1).
Т.к. данные по численности населения мы принимаем за
достаточно достоверные, можно по этим данным и с помощью
рассчитанных выше зависимостей восстановить. УДС за
промежу-точные годы. Ниже (на рис. 2) показано сопоставление
рассчитанных данных с фактическими, приведенными в табл.
Фактические данные по протяженности УДС СССР, тыс. км
|
Годы |
Протяженность сети, тыс. км |
|
|
общая |
в т.ч. с твердым покрытием |
|
| 1925 |
72 |
18 |
| 1928 |
101,6 |
24 |
| 1930 |
120,7 |
30,7 |
| 1955 |
172 |
67 |
| 1965 |
200 |
90 |
| 1970 |
220 |
110 |
| 1975 |
225 |
115 |
| 1980 |
244,5 |
141,7 |
| 1985 |
254,9 |
168,2 |
| 1990 |
273 |
187 |
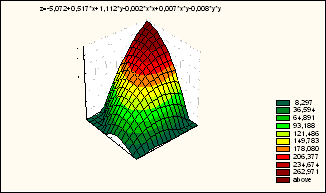
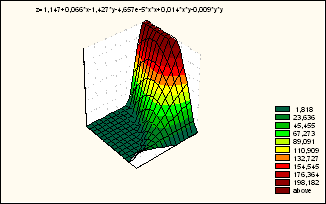
Рис. 1. Двухфакторная динамическая модель зависимости
общей протяженности УДС и с твердым покрытием
от общего и городского населения
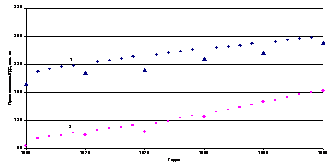
Рис. 2. Сопоставление фактических и расчетных протяженности УДС
На рис.2: 1 – общая протяженность;
2 – в т.ч. с твердым покрытием. Легенда: - расчетное
значение общей протяженности УДС, - то же, фактическое
значение; - расчетное значение протяженности с твердым
покрытием УДС, - то же, фактическое значение.
Анализ этого сопоставления показывает достаточно хорошее
соответствие. Только для общей протяженности получилось
строго систематическая небольшая ошибка. Это говорит
о том, что в статистических данных не была учтена протяженность
поселковых улиц, а в данных по населению было учтено
все. Таким образом, метод многофакторного динамического
прогнозирования де-монстрирует высокую чувствительность,
с помощью которой можно выявить недостатки официального
статистического учета.