
Рассмотрен метод определения параметров транспортного потока на нерегулируемых и кольцевых пересечениях. По мнению автора, данный метод позволит оценить параметры транспортного потока.
Одними из основных параметров транспортного
потока, влияющих на результаты применения существующих
методик, для нерегулируемого или кольцевого пересечения
являются граничный интервал и интервал следования. При
этом интервал следования представляет постоянную величину,
которая может быть определена как среднее временных
интервалов между автомобилями, начиная со второго транспортного
средства в очереди. Более сложной является процедура
определения граничного интервала.
Основоположниками в области определения граничных интервалов
были Greenshields [2] и Raff [4]. Brilon, Koenig, Troutbeck
[1] провели исследование по сравнению наиболее распространенных
методик определения граничного интервала и интервала
следования. В результате исследования, основанного на
микромоделировании транспортных потоков, установлено,
что лучшие результаты дают методики, которые разработали
Hewitt, Troutbeck, и Siegloch.. Методика Hewitt является
сложной для практического применения. Методика Siegloch
была единственной из так называемых регрессионных методов
оценки, которая больше всего соответствовала действительности;
она исходила из наличия постоянной очереди на перекрестке
во второстепенном направлении. Исследователи [1] сделали
вывод, что наиболее рациональной и с точки зрения трудозатрат,
и точности оказалась методика Troutbeck основанная на
методе максимального правдоподобия (Maximum-Likelihood-Method).
Рассмотрим поэтому ее более подробно.
Методика определения граничных интервалов на основе
метода максимального правдоподобия основана на определении
вероятности, с которой граничный интервал определенного
транс-портного средства попадает в диапазон между ai
(принятый интервал) и ri (отклоненный интервал). Эта
вероятность определяется как разница вероятностей F(ai)
– F(ri). При этом ri – это наибольший из отклоненных
одним транспортным средством интервалов. Для всех рассмотренных
транспортных средств, которыми минимум один временной
интервал был отклонен, определяется функция вероятности:
![]() ,
(1)
,
(1)
где L* – функция вероятности; F(x) – функция распределения x; ai – интервал, принятый i-ым транспортным средством; ri – максимальный интервал, отклоненный i-ым транспортным средством; n – количество рассмотренных транспортных средств; i – порядковый номер транспортного средства.
Логарифм L от этой функции определяется как:
![]() (2)
(2)
Логарифмическое преобразование подтверждает, что L и L* для одних и тех же параметров µ и σ достигнут максимума лишь в случае, если логарифмическая функция будет постоянно возрастающей. Значения параметров µ и σ рассмотренного логнормального распределения, которые соответствуют максимуму L, можно определить, используя следующие уравнения:
 (3)
(3)
и
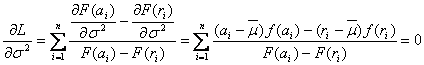 (4)
(4)
где
![]() и
и ![]() .
.
Для решения такой системы равенств Troutbeck предложил при определении параметра µ задавать какое-либо значение параметра σ2. И, наоборот, для определения параметра σ2 задавать какое-либо значение параметра µ. Итерации необходимо продолжать до момента, когда оценки параметров будут варьироваться незначительно. Такую процедуру легко можно осуществить с помощью модуля «Поиск решения» в MS-Excel. Значение математического ожидания m и среднеквадратического отклонения s2 распределения граничных интервалов можно определить, как:
и
![]() (6)
(6)
Для расчета граничных интервалов необходимо
выбрать для каждого рассмотренного транспортного средства
соответственно пары значений самого большого отклоненного
интервала и принятого интервала (транспортные средства,
которыми не было отклонено ни одного интервала, в данном
случае не учитываются [5]; не рассматриваются и те пары
значений, для которых величина принятого интервала меньше
величины отклоненного). Функцию распределения всех наибольших
отклоненных интервалов, а также функцию распределения
принятых интервалов необходимо сопоставить другом с
другом для каждого рассматриваемого не-регулируемого
пересечения. Затем методом, который был описан выше,
определяются параметры логнормального распределения.
Математическое ожидание данного распределения и будет
граничный интервал.
Для проверки методики определения граничного интервала
с помощью метода максимального правдоподобия было рассмотрено
два кольцевых пересечения в г. Иркутск. Натурные обследования
проводились с помощью видеокамеры. При этом было важно
определить такую линию (см. рис.), при прохождении которой
будет фиксироваться то или иное событие (например, момент
времени прохождения этой линии транспортным средством,
движущимся в главном направлении). Для упрощения обработки
видеоматериала был разработан программный модуль на
базе MS-Access, позволяющий быстро фиксировать все временные
интервалы (принятые и отклоненные). После обработки
программа подготавливала для каждого транспортного средства
пары значений принятого и максимального отклоненного
интервалов. Дальнейшая обработка двух полученных столбцов
осуществлялась в программах Statistica и MS-Excel.
Результаты оценки граничных интервалов, полученных по
методике с применением метода максимального правдоподобия
(рис. 1, б), представлены в таблице.
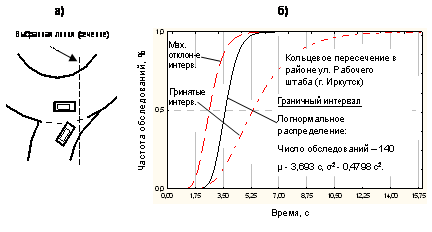
Рис.1.Исследование параметров транспортного потока на кольцевых пересечениях: а) – выбор сечения; б) - результаты оценки граничных интервалов
Значения граничного интервала и интервала следования в HBS 2001[3] выше значений, полученных в результате нашего исследования. Меньшие значения этих параметров соответствуют более высоким значениям пропускной способности второстепенного направления. Это объясняется тем, что в данном исследовании были рассмотрены крупные пересечения с уширением проезжей части на подходах, что позволяло части водителей более быстро въезжать в кольцевой поток, а так же отсутствием разметки и особенностями поведения водителей, характерными для данного региона.
Результаты оценки временных интервалов на кольцевых
пересечениях, с.
|
Место обследования |
Граничный интервал |
Интервал следования |
||
| Результаты |
HBS 2001 |
Результаты |
HBS 2001 |
|
| Кольцевое пересечение в районе ул. Рабочего штаба |
3,7 |
4,1 |
2,1 |
2,9 |
| Кольцевое пересечение в районе ул. Байкальская |
3,5 |
4,1 |
2,5 |
2,9 |
Литература
1. Brilon W., Koenig R., Troutbeck
R.J. Useful Estimation Procedures for Critical Gaps
/ Proc. of the third international Symposium on Intersections
Without Traffic Signals. Portland, Oregon, U.S.A., 1997,
pp. 71 - 87
2. Greenshields B.D., Shapiro D., Ericksen E.L. Traffic
Performance at Urban Street Intersections. Technical
Report No. 1, Yale Bureau of Highway Traffic, 1947
3. Handbuch fur die Bemessung von Stra?enverkehrsanlagen
(HBS 2001). – Forschungsgesellschaft fur Strassen und
Verkehrswesen, Koeln, Januar 2002.
4. Raff M.S., Hart J.W. A volume Warrant For Urban Stop
Signs. Eno Foundation for Highway
5. Weinert A. Grenz- und Folgezeitlucken an Knotenpunkten
ohne Lichtsignalanlagen / Schriftenreihe Lehrstuhl fur
Verkehrswesen, Heft 23, Ruhr-Universitat Bochum, 2001