
Задача восстановления матриц корреспонденций (OD matrix estimation) формулируется как поиск минимума взвешенной суммы квадратов отклонений между значениями интенсивности движения, полученными по результатам оценки, и значениями полученными по результатам обследований. Метод поиска пространства решений приводит к градиентному методу, решение которого начинается в любой допустимой точке и продолжается до поиска оптимальной. Большинство оптимизационных пакетов (MINOS, Optimization Toolbox системы Мatlab) проводят поиск решений с некоторого ограничения, продвигаясь в направлении другого. Эффективность поиска зависит от вида целевой функции задачи, от алгоритма решения и нахождения начальной точки решения (starting point).
Принимая во внимание, что первые два фактора являются постоянными, быстрый желаемый результат можно получить, если начальное предположение будет ближе к оптимальному решению. Важно отметить, что при использовании робастных (устойчивых) методов оценки, даже при некачественном начальном предположение, модель генерирует оптимальные значения: при этом скорость конвергенции будет тем выше, чем ближе предполагаемое решение к оптимальному. Начальное решение в общем случае является предположением, строящимся на информации о реальном распределении потоков. В задаче оценки OD матриц магистральных улиц исходными данными являются значения интенсивности движения по основной линии, на въездах на магистраль и выездах с нее. Кроме того, из геометрии рассматриваемой сети, могут быть получены время на передвижение по ее графам и длина перемещений. На основании этой информации рассмотрим пять методов получения начального решения (seed matrix) для оценки матриц корреспонденций.
Равномерное распределение. Метод является простейшим в генерировании начального решения. Метод «предполагает», что все потоки, движущиеся в пункты назначения, распределены равномерно. На рис. 1 в качестве примера представлена секция магистральной улицы.
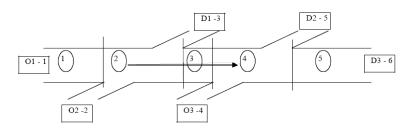
Рис.1 - Пример участка магистральной улицы
В рассматриваемом случае 3 зарождающих пункта, 3 поглощающих и 8 пересечений. Данный метод принимает, что потоки в D1, D2, D3 равномерно распределены относительно отправляющих О1, и О2; таким образом, OD пропорции составят 1/3 (33,33%), а для О3, имеющего только 2 пункта назначения (D2 и D3), 50% соответствующего исходящего потока. Учитывая условие сохранения потоков в OD матрицах, неосуществимые корреспонденции отобразим «-1». – транспортные средства движущиеся из пункта отправления не могут следовать в данный пункт назначения. Используя данное правило, OD матрица генерируется в соответствии с табл.1.
Табл. 1. Оценивание равномерным распределением
| O/D |
D1 |
D2 |
D3 |
| O1 |
1/3 |
1/3 |
1/3 |
| O2 |
1/3 |
1/3 |
1/3 |
| O3 |
-1.0 |
1/2 |
1/2 |
Метод пропорционального распределения. Метод относится к числу классических методов оценивания OD матриц. Он основан на следующей концепции: «тяготение поглощающего пункта находится в прямой зависимости от числа транспортных средств, следующих в его направлении». Другими словами, большее количество транспортных средств, движущихся в направлении принимаемого пункта, увеличивают долю суммарного числа исходящих поездок, приходящихся на этот пункт. Отсюда, для трех пунктов прибытия, пропорция числа поездок определяется на основании общего значения потока, приходящегося на соответствующий пункт. Характерной особенностью метода, является независимость от числа отправляющих пунктов. Представим исходные значения рассматриваемого участка магистральной улицы (рис.1) в виде табл.2.
Табл. 2. Данные примера магистральной улицы
| № |
Наименование |
Значения |
| 1 |
Длина секций, (м) |
200, 300, 50, 250, 400 |
| 2 |
Значение потоков, входящих в основной (центральный), (ед.) |
375, 25, 100 |
| 3 |
Значения потоков, исходящих из основного, (ед.) |
30, 70, 380 |
| 4 |
Основной поток, (ед.) |
370, 390, 350, 440, 370 |
Рассмотрим первый ряд OD матрицы. Из О1 транспортные средства движутся в направлении D1, D2, D3 с притяжением – 30, 70 и 380 соответственно. Следовательно, элементами первого ряда исходной матрицы будут 30/(30+70+380), 70/(30+70+380), 380/(30+70+380). Подобным образом оцениваются элементы второго и третьего рядов:
| O/D |
D1 |
D2 |
D3 |
| O1 |
30/(30+70+380)=0,063 |
70/(30+70+380)=0,146 |
380/(30+70+380)=0,146 |
| O2 |
30/(30+70+380)=0,063 |
70/(30+70+380)=0,146 |
380/(30+70+380)=0,146 |
| O3 |
-1.0 |
70/(70+380)=0,156 |
=80/(70+380)=0,844 |
Итеративный метод. Метод основан на алгоритме пропорционального выравнивания, разработанного в 1941 году [2]. Алгоритм рассматривается как смешанная технология пропорционального распределения, балансирующая значения входящих потоков с исходящими. Алгоритм многократно перебирает значения ячеек OD матрицы пропорционально сумме строк и столбцов до выполнения условия полной сходимости. Последовательность алгоритма расчета может быть представлена следующим образом:
Step 0
Set
![]()
![]() если обмен потоками
между ‘i’ и ‘j’ возможен.
если обмен потоками
между ‘i’ и ‘j’ возможен.
![]() если обмен потоками между
‘i’ и ‘j’ невозможен
если обмен потоками между
‘i’ и ‘j’ невозможен
Step 1
Set
![]() для всех i,
j, где
для всех i,
j, где
![]() наблюдаемые
значения в точке
‘i’ заданные для известных зависящих от
‘i’.
наблюдаемые
значения в точке
‘i’ заданные для известных зависящих от
‘i’.
Step 2
Set
![]() для всех i,
j, где ‘Dj’ наблюдаемые
исходящие значение потока в точке 'j' заданные
для всех известных,
заканчивающиеся в 'j'.
для всех i,
j, где ‘Dj’ наблюдаемые
исходящие значение потока в точке 'j' заданные
для всех известных,
заканчивающиеся в 'j'.
Step 3
If
![]() для всех i,
then STOP
для всех i,
then STOP
Else set k=k+1 and go to step 1.
Для иллюстрации работы алгоритма используем пример (рис.1) и данные табл. 2. В результате получены три промежуточных и финальная процентная OD матрица.
Табл. 4. Итерационные шаги оценки OD матрицы итеративным методом
Первая итерация
| OD 1 |
|
|
OD 2 |
|
|
OD 3 |
|
|
| 1 |
1 |
1 |
125 |
125 |
125 |
29,29 |
49,71 |
269,8 |
| 1 |
1 |
1 |
8,33 |
8,33 |
8,33 |
1,95 |
3,31 |
17,99 |
| 0 |
1 |
1 |
0 |
50 |
50 |
0 |
19,8 |
107,9 |
Вторая итерация
| OD 1 |
|
|
OD 2 |
|
|
OD 3 |
|
|
| 125 |
125 |
125 |
29,29 |
49,71 |
269,8 |
25,13 |
40,45 |
315,5 |
| 8,33 |
8,33 |
8,33 |
1,95 |
3,31 |
17,99 |
7,290 |
5,280 |
10,79 |
| 0 |
50 |
50 |
0 |
19,8 |
107,9 |
0,00 |
32,40 |
63,30 |
Третья итерация
| OD 1 |
|
|
OD 2 |
|
|
OD 3 |
|
|
| 25,13 |
40,45 |
315,5 |
25,13 |
40,45 |
315,5 |
25,13 |
40,45 |
315,5 |
| 7,290 |
5,280 |
10,79 |
7,290 |
5,280 |
10,79 |
7,290 |
5,280 |
10,79 |
| 0,000 |
32,40 |
63,30 |
0,000 |
32,40 |
63,30 |
0,000 |
32,40 |
63,30 |
Финальная OD матрица
| O/D |
D1 |
D2 |
D3 |
| O1 |
0.0659 |
0.1061 |
0.8278 |
| O2 |
0.3120 |
0.2262 |
0.4616 |
| O3 |
-1.0 |
0.3385 |
0.6615 |
Гравитационные модели являются первыми моделями распределения потоков. Основным параметром гравитационных моделей является функция импеданса. Разработанные идеи [3] были положены в основу гамма распределения, связывающей понятия о том, что вероятность долговременных и кратковременных поездокна магистральных улицах очень низка. Следовательно, вышеуказанное предположение может быть описано гамма-распределением:
![]()
где Fij - фактор тяготения между пунктами ‘i’ и ‘j’;
![]() - коэффициент
кривой, форм фактор =1,5;
- коэффициент
кривой, форм фактор =1,5;
![]() - параметр размера
=
- параметр размера
=
![]() (среднее расстояние поездки); dij – расстояния между парами (i,j);
avg.trip length=(1/T)∙∑(длина звена)∙(значение
потока); T – сумма генерируемых поездок
(среднее расстояние поездки); dij – расстояния между парами (i,j);
avg.trip length=(1/T)∙∑(длина звена)∙(значение
потока); T – сумма генерируемых поездок
Значения входящего потока OD матрицы определяются как:
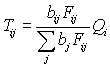
где Tij – взаимообмен между
парами (i,j); bj – фактор
баланса от итераций; Qj -
исходящий поток; Dj -
входящий поток; Qj и
Dj – поток отправления и прибытия при ограничениях
![]()
В предложенном алгоритме фактор баланса
игнорируется, поскольку в нашей задаче требуется первоначальное решение,
а не точная оценка.
Используя рис. 1.
и данные табл. 2., рассмотрим
работу метода на примере. Основной параметр
![]() принимаем 1,5.
принимаем 1,5.
Среднее расстояние поездки =
(370*200+390*300+350*50+440*250+370*400)/(375+25+100)=933
метра. Параметр гравитационной модели
![]() . Используя эти параметры и матрицу расстояний (табл.
5) оценим множители импеданса (табл. 6).
. Используя эти параметры и матрицу расстояний (табл.
5) оценим множители импеданса (табл. 6).
Табл.5. Матрица расстояний
| O/D |
D1 |
D2 |
D3 |
| O1 |
500 |
800 |
1200 |
| O2 |
300 |
600 |
1000 |
| O3 |
0 |
250 |
650 |
Табл.6. Матрица сопротивлений (импедансов)
| O/D |
D1 |
D2 |
D3 |
| O1 |
0,0008325 |
0,0008122 |
0,0005050 |
| O2 |
0,0005701 |
0,0008692 |
0,0006671 |
| O3 |
0,000 |
0,0004650 |
0,0008686 |
Табл. 7. Результирующая матрица
| O/D |
D1 |
D2 |
D3 |
| O1 |
0,1793 |
0,3328 |
0,4878 |
| O2 |
0,1093 |
0,3170 |
0,5736 |
| O3 |
-1,0 |
0,1850 |
0,8150 |
Метод включения процентовсчитается интуитивным методом оценки OD матриц. Метод, основан на генерировании процентов и предполагает, что на любом поглощающем пункте изменение доли притяжения не зависит от места происхождения потока. Следовательно, путем отслеживания изменения процентов на каждой секции, рассчитывается процентная OD матрица. Для последней секции, являющейся последним пунктом притяжения, процент отворота назначается 100%.
Первоначально рассчитывается процент отворота на каждой секции. Секция, определяется как часть магистральной улицы, расположенная между входящими и исходящими пунктами таким образом, что верхняя часть потока заканчивается на входящем пункте, а нижняя - на исходящем. С учетом этого условия, рассматриваемая часть магистрали слагается из 5 секций, для которых проценты отворота составят соответственно 0; 7,69; 0; 15,9; 100. Первоначально элементы OD матрицы задаются для каждого отправляющего пункта, перемещаясь вниз по направлению основного потока, назначаются в соответствии с «процентами отворота» на каждом исходящем пункте отслеживая отвороты автомобилей. Результативная матрица представлена в табл.8.
| O/D |
D1 |
D2 |
D3 |
| O1 |
0,0769 |
0,159∙(1-0,0769)=0,1468 |
1-0,159-0,0769=0,7763 |
| O2 |
0,0769 |
0,159∙(1-0,0769)=0,1468 |
1-0,159-0,0769=0,7763 |
| O3 |
-1,0 |
0,159 |
1,0-0,159=0,841 |
Первоначальная OD матрица оценивается на основе замеров интенсивности движения определенного временного интервала. Таким образом, процесс генерирования исходных OD значений является совокупным значением замеров интенсивности потока всех временных интервалов.
Литература
1. Михайлов А.Ю., Головных И.М. Современные тенденции проектирования и реконструкции улично-дорожных сетей городов. – Новосибирск: Наука, 2004. - 267 с.
2. Deming, W., E. and Stephan, F., F. On a least squares adjustment of a sampled frequency table.
May, D, A. and Willis E.A. (1981) Deriving origin-Destination information from routinely collected traffic counts – Vol. I, research report UCB-ITS-RR-81-8.
4.. Henk J. van Zuylen and David M Branston. Consistent link flow estimation from counts. Transportation Research, Vol. 16B, 1982, pp. 473 – 476.
5.Davis, G (1994). Dynamic estimation of origin-destination patterns in Freeways, Final report MN/RC-94/18.