
В зарубежной теории и практике проектирования
транспортных систем уже с 70-х годов уделялось большое внимание
методам восстановления матриц существующих корреспонденций
(Estimation of Origin-Destination Matrix from Traffic Counts),
которые отнесены специалистами “Мировой дорожной ассоциации”
(PIARC) к числу важнейших инструментов анализа УДС. В руководстве
«Highway Capacity Manual 2000» [6] в гл. 29 “Corridor analysis”
изложен метод такой оценки применительно к магистральным
дорогам. По данной тематике имеется обширнейшая библиография.
В нашей стране в первую очередь получила развитие теория расчетов
пассажиропотоков, в том числе, были предложены методы оценки
существующих матриц корреспонденций на маршрутном пассажирском
транспорте [1]. Собственно методам восстановления матриц
корреспонденций в виде потоков транспортных было посвящено
несколько исследований [3,4], что объяснялось относительно
меньшим интересом к проблемам проектирования и реконструкции
УДС.
Рост автомобильного парка и объемов движения в российских
городах требует совершенствования инструментария проектирования
и оценки УДС. Поэтому представляется необходимым рассмотреть
возможности решения рассматриваемой задачи применительно
к российским условиям, учитывая, в первую очередь применяющиеся
методы обследований интенсивности движения. Как правило, такие
обследования проводятся в пиковые часы с подсчетом транспортных
средств разных типов на всех направлениях движения на каждом
из обследуемых перекрестков. Поэтому формулируется задача
регрессионной оценки матрицы корреспонденций для следующих
условий:
· исходными данными являются замеры интенсивности движения
на отдельных участках УДС, выполняемые в определенное время
в будние дни (например, вечерний пик 17—19ч.);
· исходные данные об интенсивности движения содержат ошибки,
вызванные проведением замеров в разные дни и ошибками самих
подсчетов интенсивности движения.
Следует привести очень важную для понимания рассматриваемой
задачи цитату из [6,с.29-30]: “Количество элементов матрицы
корреспонденций всегда превосходит количество сегментов сети.
Цель оценивания состоит не в определении точной матрицы корреспонденций,
а в нахождении такой, которая достаточно близка к ней и соответствует
данным интенсивности движения” (под сегментами в оригинальном
тексте понимаются дуги графа, которым представлено описание
сети). В отличие от [6] нами рассматривается не “транспортный
коридор”, а участок УДС. С целью распределения потоков по
принципу “все или ничего” (all or nothing) УДС разделяется
на отдельные “маршруты”, или (как в [6]) “направления движения”
(рис.1,2). Таким образом, матрица, описывающая принадлежность
корреспонденций дугам графа, будет состоять из 1 и 0 (наличие
или отсутствие данной корреспонденции).
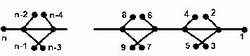
Рис. 1. Представление одного из направлений движения на улице или дороге в виде графа для определения матрицы корреспонденций: 1,2,…,n - вершины графа, в которых возникают и заканчиваются кор-респонденции
Отдельно рассматриваемое направление движения
(маршрут) представляется в виде графа, для которого определяется
своя матрица корреспонденций. Соответственно начальными
и конечными пунктам корреспонденций являются поворотные
потоки на перекрестках, т.е. входящие потоки на улицу или
выходящие с нее (рис.1). Вместо центроидов РТР используются
“нагрузочные” вершины сети (рис.2), образующиеся на границах
рассматриваемого участка УДС, в которых начинаются и оканчиваются
корреспонденции.
Сформулированная задача регрессионного оценивания корреспонденций
предполагает использование статистических процедур, устойчивых
к выбросам (т.е. грубым ошибкам данных).

![]()
| а) вершины матрицы корреспонденций транзитных потоков (“загрузочные” вершины) центра Иркутска и интенсивности движения в вечерний час пик, физ.ед/ч | 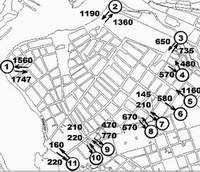 |
| б) граф для оценки матрицы корреспонденций из вершины 1 в вершины 1,2,3,…, 20, используемой для оценки транзитных потоков из вершины 5 в вершины 1,2,3 | 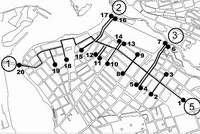 |
| в) транзитные потоки из вершины 5 в вершины 1,2,3, полученные при оценке матрицы корреспонденций для графа УДС, представленного вершинами 1,2,3, …, 20 | 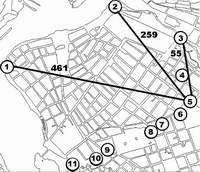 |
Рис. 2. Определение матрицы корреспонденций для транзитных потоков в центральной части Иркутскаа) исходные потоки на водах и выходах в центральную часть города, для которых рассчитывается матрица корреспонденций;б) один из маршрутов движения, на которые разделяется УДС, и для которых строятся графы и рассчитываются матрицы корреспонденций;в) результат оценки транзитных потоков, для одного из входов в центральную часть



Восстановление матриц корреспонденций можно
выполнять с использованием функций:
LP библиотеки Optimization Toolbox 2.0 версий пакета MATLAB
5.1 и 5.2;
LINPROG библиотеки Optimization Toolbox 2.2 версии пакета
MATLAB 6.1
Выбор пакета MATLAB для решения задачи восстановления матриц
корреспонденций обусловлен тем, что пакет:
ориентирован на выполнение операций с векторами и матрицами,
в том числе, разряженными матрицами;
применяется для решения сетевых задач [7], в том числе,
на его основе осуществляется разработка приложений для транспортных
задач, например, программа DelftOD Version 2.0 (автор Nanne
J. van der Zijpp, Delft University of Technology - http://
www.delftod. tudelft.nl);
достаточно известен и распространен в нашей стране, имеет
сопровождение.
Следует отметить, что опубликованное в августе 2003г. решение
задачи восстановления матриц корреспонденций в информационных
сетях [7] также использует в качестве начальной итерации
гравитационную модель, но следующей итерации рассматривается
задача томографии, решаемая методами квадратичного программирования,
т.е. применяется взвешенный метод наименьших квадратов.
В нашем случае маршруты (рис. 1,2) описываются матрицами,
имеющими плохую обусловленность, поэтому тесты по использованию
взвешенного метода наименьших квадратов (1998-2001гг.) показали
его непригодность.
Литература
1.Артынов А.П., Скалецкий И.И. Автоматизация
процессов планирования и управления транспортными системам.
- М.: Транспорт, 1981. – 280 с.
2.Демиденко У.З. Линейная и нелинейная регрессия. – М.:
Финансы и статистика, 1981. – 302 с.
3.Киселева О.Н., Сена С.Л., Федоров В.П. Определение матрицы
существующих грузовых корреспонденций на основе обследований
на магистральной сети. //Социально-экономические проблемы
развития транспортных систем городов. Тез.докл. второй
обл. эконом. конф. -Свердловск, 1988. с. 95 - 98.
4.Мягков В.Н., Пальчиков Н.С., Федоров В.П. Математическое
обеспечение градостроительного проектирования. – Л.: Наука,
1989. – 144 с.
5.Петрович М.Л. Регрессионный анализ и его математическое
обеспечение на ЕС ЭВМ: Практическое руководство. – М.:
Финансы и статистика, 1982. – 199 с.
6.Highway Capacity Manual. // TRB, Washington, DC, 2000.
– 1134 p.
7.Yin Zhang, Roughan M., Duffield N., Greenberg A. Fast
Accurate Compu-tation of LargeScale IP Traffic Matrices
from Link Loads. SIGMETRICS’03, 2003, June 10–14, 12 p.
Available: http://www.research.att.com