Учитывая специфику сбора данных о транспортных потоках, предлагается обзор методов калибровки данных обследования интенсивности движения
Основной для выполнения проектов ОДД и имитационного моделирования потоков являются данные интенсивности движения, замеры которой обычно выполняются на перекрестках в пиковые часы с подсчетом интенсивности движения по отдельным направлениям. При использовании данных обследований интенсивности движения на отдельных элементах сети, неизбежно возникают ошибки: по данным замеров на смежных перекрестках величины входящего и выходящего потоков имеют разные значения. Эти ошибки вызваны проведением замеров в разные дни и ошибками самих подсчетов (рис. 1):
|
|
|
Рис.1. Схема входящего и выходящего потоков
Учитывая специфику сбора данных о транспортных потоках в российских условиях, в статье предлагается обзор следующих методов калибровки данных интенсивности потока: 1) наименьших квадратов; 2) максимального правдоподобия; 3) размытой регрессии; 4)метод размытой оптимизации; 5) интервальный регрессионный.
Алгоритм задач можно представить следующим образом: даны значения интенсивности потоков на дугах транспортной сети. Необходимо откорректировать значения потоков с учетом сохранения баланса и других ограничений.
Метод наименьших квадратов (МНК) основан на минимизации суммы разностей квадратов между наблюдаемыми и оцененными значениями интенсивности потоков:
(1)
при условии сохранения потоков и других ограничений. Для больших сетей метод может оказаться слишком громоздким в вычислительном отношении, однако не требует дополнительных предположений и допущений. Он может быть приведен к взвешенному МНК, в котором веса определяют для каждого квадратного члена.
Табл. 1. Методы уравнивания данных интенсивности транспортного потока на сетях
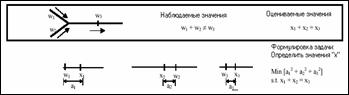
1 - Схематичное представление для МНК; 2 - Метод максимального правдоподобия; 3 - Метод «размытой» регрессии; 4 - Методом «размытой» оптимизации; 5 - Интервальный регрессионный метод
Метод
максимального правдоподобия используют,
когда наблюдаемое значение
можно представить
в виде случайного, распределенного
с вероятностью
, где
- параметр распределения
вероятности, подлежащий оцениванию. Необходимо определить
такие параметры распределения
, при которых
вероятность получения наблюдаемых значений будет максимальной,
с учетом соответствующих ограничений
на
. Van Zuylen и Branston [3] предложили
функцию вероятности
, зависящую только от значений
и
, и предложили оценивать параметры в виде:
, (3)
следовательно:
(4)
Приняв,
- распределение
Пуассона, решением задачи будет:
(5)
где
- множитель Лагранжа, определяется заменой решения (5)
ограничениями (например,
и т.д.). Индекс
определяет число ограничений. В случае
- функция нормального
распределения с постоянной дисперсией
(
), решение (5) эквивалентно решению МНК (1), если дисперсия
для каждого наблюдаемого значения
различна (учитывается
величина разности между замерами) решение сводится к
решению взвешенного МНК.
Для риc.1
целевая функция:
при условии:
,
,
,
Если
принимается как
функция распределения Пуассона, на оцениваемые параметры
ограничения по знаку не налагаются.
|
|
|
|
|
|
|
|
|
|
|
|
||
Где значение
определяется
решением системы ограничений
|
для
|
|
|
| для
для
|
|
|
Willumsen и van Zuylen [3,4] первоначально использовали данный алгоритм для определения матриц корреспонденций транспортных потоков. Для того чтобы решение сходилось, необходимо условие сохранения потоков. Принималось, что суммарный объем исходящего потока равнялся входящему. С логической точки зрения этот метод наиболее подходит в случаях независимости и случайности наблюдаемых значений. В нашем случае значения потоков на дугах графа сети коррелированны.
Willumsen [4] модифицировал метод до максимизации
энтропии, аналогичной МНК (который, в свою очередь,
эквивалентен методу максимума правдоподобия, при
) с весами.
Метод
«размытой» регрессии подобен
методу максимального правдоподобия.
Различие в том, что вместо функции распределения
вероятности, метод предполагает
наличие некоторого размытого разброса данных (fuzzy cloud) с
центром
. Под размытостью понимается «около
», даже если значение
неизвестно. Центром
функции принадлежности «около
», принимается оценка
. При этом
принадлежит размытому
множеству, близость которого
к
определяется
величиной
. Метод сводится к поиску оценок
максимизирующих
для всех
, при минимальном
и соответствующих ограничениях. Ввиду чего, функция
принадлежности отображает допустимое отклонение между
и
:
для всех
, (6)
где
- оценка близости
к
, в размытом множестве;
По образу треугольника, функция принадлежности имеет экстремум в
и определяется справой
и слевой
сторон треугольника:
для
и
для
соответственно,
- основание треугольника
(устанавливается аналитически).
Для риc.
1 целевая функция имеет
вид:
, при ограничениях:
,
для всех
, где
для всех
;
для всех
;
;
;
.
Метод
«размытой» оптимизации относится
к группе задач, в которых исходные данные рассматриваются
как аппроксимированные, оценки которых расположены внутри
некоторого интервала наблюдаемых. Здесь используется
понятие «приближенное
», как размытое множество около
. Первоначально идея метода заложена Kikuchi [5] и в дальнейшем усовершенствована совместно с Miljkovic
[5]. Предполагается наличие функции принадлежности размытого множества
вокруг
, внутри которого расположены значения оценок. Функция
принадлежности определяется аналитически в зависимости
от допустимого отклонения
между
и
. Необходимо отметить, метод размытой регрессии использует
функцию принадлежности
, в то время как метод размытой оптимизации
. Это различие
определяет степень «размытости»
в наблюдаемых значениях и в оценках соответственно,
что приводит к разным экстремумам функции принадлежности
рассмотренных методов.
Задав функцию принадлежности «около
», величиной
, оценки
могут быть получены
двумя способами: максимум при минимуме
; максимум суммы
:
|
|
(7) |
при условии сохранения потоков и других ограничений.
В обоих случаях алгоритм решения представляет
собой задачу линейного программирования. В табл. 1 задача
формируется следующим образом: для
целевая функция
; в случае
целевая функция:
,
при условии:
;
для
;
;
;
, где
и
отображают правую
и левую стороны треугольной функции принадлежности, соответственно:
для всех
для всех
, где
- основание функции принадлежности.
Интервальный регрессионный метод . В нем отдельные значения
конвертируют в диапазон (
) – диапазон достоверности, в котором исследуются оценки
при условии
соответствующих ограничений. В свою очередь оценки
расположены в интервале
Алгоритм сводится
к нахождению таких оценок
, при которых достигается
максимум суммы диапазонов
.
(8)
при условии:
;
для всех
и других ограничений накладываемых на исследуемые потоки, где
интервал данных
. Значение
принимается аналитически
в зависимости от достоверности
данных.
диапазон оценок с центром
.
Для риc. 1 целевая функция
задачи:
, при условии
;
для
;
;
;
,
.
В случае отсутствия предварительной информации о достоверности исходных данных справедливо использовать однородный диапазон, пределы которого устанавливаются аналитически с учетом неопределенности данных. Слишком узкий интервал разброса, может оказаться не пригодным для решения задачи. Слишком большой приведет к значительным расхождениям между наблюдаемыми и рассчитанными значениями интенсивности потока.
Среди вышерассмотренных
методов первые два являются легко интерпретируемыми,
поскольку относятся к классу классических задач по оценке
параметров. Метод размытой регрессии наибольшим образом
подойдет, если оценки
носят статистической характер, если зависимость между
и
определяется
функцией вероятности.
Последние два метода направлены на поиск оценок в некотором диапазоне исходных данных, устанавливаемого аналитическим путем в зависимости от достоверности данных и допустимого разброса между наблюдаемыми и оцененными значениями интенсивности потока. Метод размытой оптимизации может учитывать «мягкие» ограничения относительно взаимосвязи исходных данных. Введение таких предположений в модель возможно благодаря теории «размытого» множества. Интервальный регрессионный метод производит поиск решения внутри жестко ограниченного диапазона исходных данных и не может включать «мягкие» условия. Данный метод, как правило, используется в случае низкой достоверности исходных данных.
Литература
1. Zhao, M., Garrick, N. W., and Achenie, L.K., Data Reconciliation- Based Traffic Count analysis System, Transportation Research Record, 1625, TRB, National Research Council, Washington, D.C., 1998, pp. 12-17.
2. Henk J. van Zuylen and David M Branston. Consistent link flow estimation from counts. Transportation Research, Vol. 16B, 1982, pp. 473 – 476.
3. Henk J. van Zuylen and Luis G. Willumsen. The Most Likely Trip Matrix Estimated From Traffic Counts. Transportation Research, Vol. 14B, 1980, pp. 281-293.
4.
Kikuchi,
S. and Miljkovic, D. A Method to Pre-process Observed
Traffic Data for Consistency: Application of Fuzzy optimization
Concept. Presented at the 78th Annual Meeting of the
Transportation Research Board,
