
Колебания пассажиропотоков отличаются определенной закономерностью. Целесообразно
применить для расчета величины пассажиропотока математические
и вероятностно-статистические методы. Функция распределения
пассажиропотока во времени, полученная путем статистической
обработки данных, имеет ярко выраженный гармоничный характер,
и как любой периодический процесс может быть представлена
в виде тригонометрического ряда, в частности ряда Фурье.
Предложено
описывать значение объема перевозок в единицу времени (1
час) выражением (1), а его составляющие – (2-4):
Z(t) = Zo+ Zc(t)+ Zн(t)+ Zм(t), (1)
где
Zo – среднегодовое значение объема перевозки в единицу
времени;
Zc(t), Zн(t), Zм(t) – соответственно
суточные, недельные и сезонные составляющие колебания объемов
перевозок.
Zc(t) = ![]() ;
(2)
;
(2)
Zн(t) = 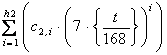 ;
(3)
;
(3)
Zм(t) = ![]() .
(4)
.
(4)
Подставив
уравнения (2) – (4) в (1) получаем выражение
Z(t)= Zo+ ![]() +
+ 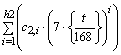 +
+
+
![]() ,
(5)
,
(5)
где ![]() – коэффициенты многочлена
Фурье;
– коэффициенты многочлена
Фурье;
![]() – коэффициент степенного
многочлена i-й степени;
– коэффициент степенного
многочлена i-й степени;
![]() – порядок многочлена
Фурье;
– порядок многочлена
Фурье;
![]() – порядок степенного
многочлена;
– порядок степенного
многочлена;
t – текущее значение календарного времени с отчетом от
начала года в часах;
24, 168, 2184 – принятые периоды колебаний объемов перевозки
в единицу времени (часовой интервал) соответственно суточный,
недельный и сезонный.
![]() – дробная часть, полученная в результате деления.
– дробная часть, полученная в результате деления.
Установлено,
что изменение объемов перевозок по дням недели удовлетворительно
описывается параболической функцией второго порядка.
Коэффициенты
уравнений многочлена Фурье определяются зависимостями (6-8):
![]() (6)
(6) ![]() (7)
(7) ![]() (8)
(8)
где yэi - экспериментальные значения объема
перевозок в i-х расчетных точках.
При проведении расчетов номера гармоник, включаемые в уравнение,
принимались адаптивно или по максимуму значения статистики
критерия Фишера F или по минимуму коэффициента средней линейной ошибки аппроксимации
E. Гармоники, которые вызывают уменьшение значения F или
увеличение значения E, не включались в модель связи. При
этом верхнее значение номера гармоник принималось не более
чем n/2.
Расчеты
по результатам обследований пассажиропотоков на маршрутной
сети г. Гомеля, подтвердили по критерию Фишера справедливость
гипотезы об использовании многочлена
Фурье для расчета часовых пассажиропотоков на маршруте:
![]() (9)
(9)
Полученная зависимость имеет высокий коэффициент множественной корреляции. Расчетная статистика критерия Фишера имеет значение больше табличного. Коэффициент средней линейной ошибки аппроксимации находится в пределах нормы.