23. Коэффициент компактности города

Так как среднее расстояние в круговом городе составляет 1/3 его диаметра, то для города площадью F км2 минимально возможное среднее расстояние будет 0,37  км. Поэтому, если фактическое среднее расстояние в городе площади F км2 составляет d км, то коэффициент компактности плана города можно определить так:

                                                                                                                      (51)

Практически могут возникнуть затруднения с определением средн6его расстояния a, так как брать большое число близко расположенных точек обременительно. Если условиться поэтому, что берутся расстояния лишь большие 1 км, то формула (51) должна быть изменена. По (48) – среднее расстояние в круге свыше 1 км составляет приближенно:

                                                                                                                    (52)

В круге диаметром в 10 км оно составит 4 км, в круге диаметром в 20 км соответственно – 7,5 км.

Поэтому вместо (51) удобнее пользоваться такою формулой.

                                                                                                        (53)

Здесь F - площадь города в км2 и a>1 - cреднее расстояние в городе свыше 1 км.

Так как площадь селитебных районов Москвы в тех границах, в которых строилась кривая распределения расстояний (рис. 21), составляет 106 км2, среднее же расстояние свыше 1 км, определенное по тому же чертежу, составляет 6,56 км, то для Москвы – на первый взгляд такого компактного города – коэффициент компактности =1,45. Для Уфы, где по черт. 20 среднее расстояние свыше 1 км составляет 9,1 км, а площадь 30,85 км2, коэффициент компактности равен 3,2, что надлежит признать совершенно неудовлетворительным. Коэффициент компактности всегда больше 1; чем ближе он к 1, тем экономнее планировка.

 

24. Распределение передвижений по дальности местожительства

В основе всей концепции, которую мы развиваем, лежит идея. Что жители города сообразуют свои передвижения с расстояниями в такой мере, что это сказывается на статистической картине распределения, с одной стороны, расселения относительно мест постоянного тяготения, т.е. главным образом – мест труда, с другой – передвижения по многочисленным бытовым и культурным поводам. Таким образом, мы полагаем, что в основе и трудовых передвижений, и культурно-бытовых передвижений, лежит качественно одно и то же правило. Однако, количественно они могут быть разными. И это совершенно естественно: очевидно все интересы, которые пробуждают население к передвижению, могут быть как-то разделены по своей силе и принудительности – одни являются, безусловно, обязательными, независимо от расстояний, другие будут ограничиваться расстоянием в большей или меньшей мере.

Представляло бы значительный планировочный интерес изучить на опыте навыки населения в этом отношении. Это способствовало бы установлению рационального, а не произвольно назначаемого, радиуса действия, а отсюда и оптимального размера разного рода общественных устройств, не говоря уже о том, что такие данные были весьма полезными при проектировках транспорта. Почин в этом отношении положен инж. Кругляковым Ю.Г., изучавшим распределение посетителей кино, бань, садов, катков и парков в Ленинграде. Некоторые из его данных мы приводим на черт. 24, 25 и 26. Интересно, что – как и следовало ожидать – предельная дальность посещения бытовых и культурных учреждений статистически меньшая, нежели предельная дальность трудовых передвижений. Опираясь на данные опроса Круглякова, мы приходим к заключению, что например, предельная дальность посещения кино – ½ часа, бань – 20 мин., а районных садов Ленинграда только 10 минут.

 

 

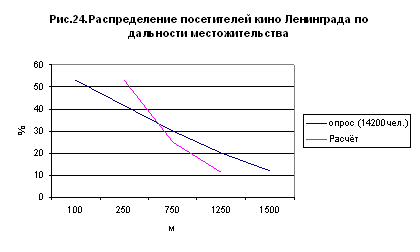
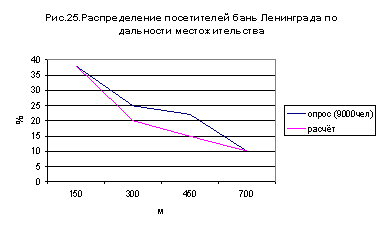       Все эти посещения лежат в зоне пешеходной доступности. Чрезвычайно интересно отметить, что наше предположение об общности логарифмического правила распределения посетителей по дальности их местожительства оправдываются опросом Круглякова. На тех же графиках (рис. 24-26) нанесены и расчетные данные, полученные по логарифмическому правилу:

                                                                                                               (54) 

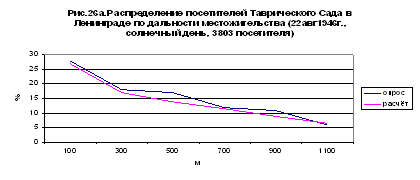
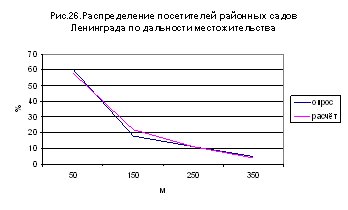       Они достаточно близки к опросным данным. Так  как транспорт интересуют поездки всех назначений, а не только трудовых, то возникает вопрос, какому же  правилу  следует суммарно распределение посетителей всех категорий по дальности их местожительства? Ближайшее рассмотрение соответственной математической  задачи приводит к заключению, что и в этом комплексном случае распределение посетителей выражается логарифмическим правилом (54), но суммарная предельная дальность  оказывается зависящей от всех предельных дальностей  посетителей различных мест тяготения. В этом нетрудно убедиться. Рассмотрим случай других потоков посетителей с предельной дальностью   и , и пусть соотношение общей численности этих посетителей выражается долями единицы a и b. Тогда суммарное распределение будет следующим:

 

                                       ,                                                        (55)

что легко позволяет произвести следующие преобразования

,

где , 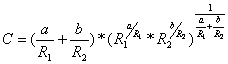.                                   (56)

Например, полагая на трудовые передвижения 60% (с предельной дальностью   км и на культурно- бытовые- 40% (с предельной дальностью  км),  получим для зоны совместного потока такое распределение:

.

Мы не имеем в настоящее время данных для установления всех составляющих суммарной логарифмической кривой распределения посетителей городских мест тяготения по дальности их местожительства. Можно надеяться, что в дальнейшем мы будем располагать такими данными. Во всяком случае, в настоящее время мы вынуждены характеризовать движение в городе некоторой средней  предельной дальностью перемещения, которая приводит к наиболее близкому представлению реального распределения перемещений в той области расстояний, где движение еще значительно. Наши расчеты, поэтому лишь приближенны. Но это вполне допустимо  при той значительной флуктуации распределения, которую мы выше рассматривали. 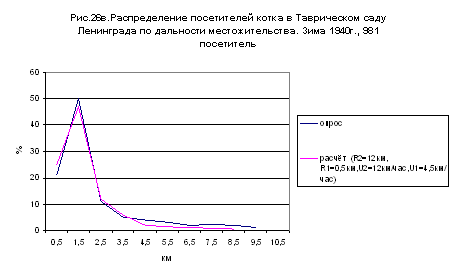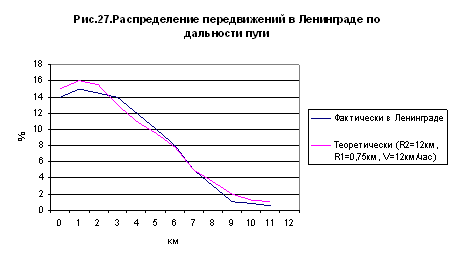Так, как мы видели, в современных условиях расселение и распределение пассажиров по дальности поездки в Москве и Ленинграде практически вполне удовлетворительно представляются предельной дальностью поездки в 1 час, что отвечает приблизительно расстоянию в 12 км.

Один из примеров  такого соответствия представлен на рис. 27.

25. Распределение пассажиров по дальности поездки

Зная правило распределения передвижений по дальности, о чем мы только что  говорили, можно получить и кривую распределения пассажиров по дальности поездки. Для этого, очевидно, достаточно учесть вероятность пользования транспортом на близких расстояниях. Выше мы рассматривали этот вопрос. В целях вычислительных удобств, мы заменим данную выше логарифмическую форму вероятности пользования транспортом на близких расстояниях следующей эмпирической формулой:

 

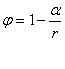                                                                                                                                   (57),

где r- расстояние в км, а a - параметр. Мы будем в дальнейшем принимать его равным 0,5. это соответствует такому ходу вероятности пользования транспортом:

км

0,5

1

2

3

4

5

6

вероятность

0

0,5

0,75

0,83

0,88

0,9

0,92

 

Теперь легко составить уравнение кривой распределения пассажиров по дальности поездки в дифференциальной форме:

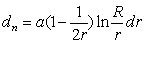                                                                                                                 (58)

 где                                                                                           (59)                                                                                                                               

То же уравнение в интегральной конечной форме, пригодной для непосредственных вычислений, имеет следующий вид:

                                        ,                        (60)

где - знак подстановки, т.е. разности значений стоящей справа функции расстояния r при верхнем пределе  и нижнем пределе . Вот вывод этих формул. Относительное число поездок в интервале расстояний dr по /54 и 57/ будет

                                                                                                                   (а)

Найдем число всех поездок в интервале расстояний от 1 км до R.

 

Находим  , что при a=0,5 дает

                                        .                                                       (б)

Деля (а) на (б) и умножая на 100, получаем (58 и 59), данные в тексте. Интегрируя (58) найдем интегральную формулу (60) той же кривой, данную в тексте.

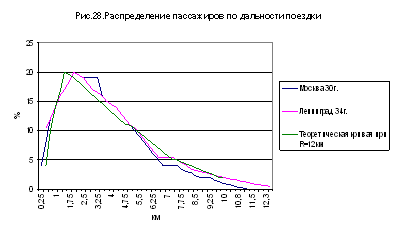         На рис. 28 показано, насколько близко эта теоретическая кривая распределения пассажиров по дальности поездки ложится к фактическим правилам распределения пассажиров по дальности поездки в Москве и Ленинграде (последние взяты у Зильберталя: Проблемы городского пассажирского транспорта, 1937 г., стр. 27). Нельзя не видеть в этом хорошего подтверждения развиваемой теории.

 

26. Средняя дальность поездки

Теперь легко получить и весьма важную при расчете городского пассажирского транспорта величину - среднюю дальность поездки:

                                             км                                                (61)

При r = 12 км, по этой формуле получаем км, что близко к средней фактической дальности поездки в Москве и Ленинграде – 3,97 км.

Формула эта получается  по (58 и 59) так:

,

что после подстановки из (59) и даст данную в тексте формулу. Интегрирование легко приводится по частям.

Напомним, что в этой формуле R – предельная дальность поездки в км. Но, как мы знаем, предельным является не расстояние, а время. Предельное время поездки мы принимаем в 1 час. Таким образом:

                                                              R=VT,                                                                           (62)

где  V- скорость сообщения в км/час и Т - предельная дальность поездки в часах. При Т= 1 часу, формула (61) заменится следующей:

                                                                                                 (63)

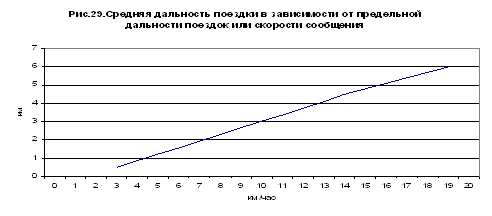
Теперь непосредственно видна зависимость средней дальности поездки от принятого в городе транспорта и плотности его сети, что вместе определяет скорость сообщения. Так, при скорости сообщения в 20 км/час, средняя дальность поездки будет 6,2 км. Ход соответствующей кривой представлен на рис. 29.

В соотношении  формул (63 и 61), выражающих среднюю дальность поездки, надлежит сделать важное замечание. Формула (61), выражающая среднюю дальность поездки  через предельную дальность поездки, должна применятся при R<VT, т.е. в относительно небольших городах, в которых максимальное  расстояние преодолевается с помощью существующих средств сообщения скорее, нежели  предельная продолжительность поездки. В этом смысле небольшие относительно города имеют среднюю дальность поездки, определяемую предельной дальностью поездки. Города  большие, для которых R>VT имеют среднюю дальность поездки, определяемую не размерами города, а скоростью сообщения, т.е. формулой (63). Диаметр Москвы, для которой предельная дальность поездки около 12 км, равен приблизительно 19 км (см. рис. 21).

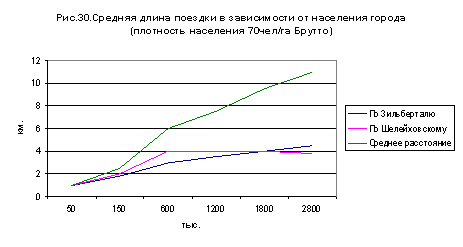
С ростом города, при стабильных по скорости средствах сообщения, средняя дальность поездки, стремятся к некоторому пределу. Это не всегда достаточно принимается и учитывается. Ошибку этого рода делает, в частности, и Зильберталь, давая свою эмпирическую формулу для определения средней дальности поездки в виде:

 

где F- площадь города1.

Сравнение формулы Зильберталя с предложенными в этой работе дано на рис. 30, где показано также и среднее расстояние в соответствующих городах. Как видим, дальность поездок весьма отстает от расстояний, встречающихся в городах, по мере их роста.

 


1Зильберталь. Проблема городского пассажирского транспорта, 1937, стр. 26.